製造業で品質管理の仕事をしていると、工程能力を計算することがあります。そのとき正規分布やバラツキσ(シグマ)という言葉がよくでてきます。
- 工程能力は1.33以上必要・・
- 工程能力が1.67以上あると安定してる・・
- 正規性がないと工程能力を計算しても意味がない・・

正直、何いってるか分かんないんだよなぁ
って思うことありませんか?^^
この記事では、正規分布という言葉を始めて聞いたという人に簡単なイメージをお伝えします。
専門的には間違っているかも知れませんが、だいたいこんな感じ!というイメージを持って頂ければと思います。
正確で専門的なことが知りたい人向けではありませんので、ご了承下さい。(^^;;;
- 正規分布をはじめて聞いた人
- 工程能力がさっぱり理解出来ない人
音声で学びたい人はこちら
正規分布って何?


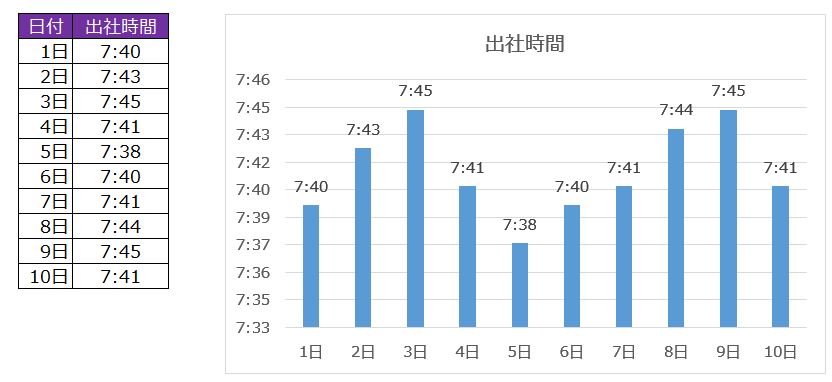
これを見ている人は、会社勤めをされてると思いますので、会社の出社時間(タイムカードを切った時間)で具体的な例を考えてみます。
朝7時に家を出て会社まで約40分通勤する人を考えます。
1~10日までの出社時間を記録してみます。毎朝7時に家をでたとしても、信号待ちや途中の混み具合で会社に着く時間は前後します。
このグラフの見方を少し変えてみます。
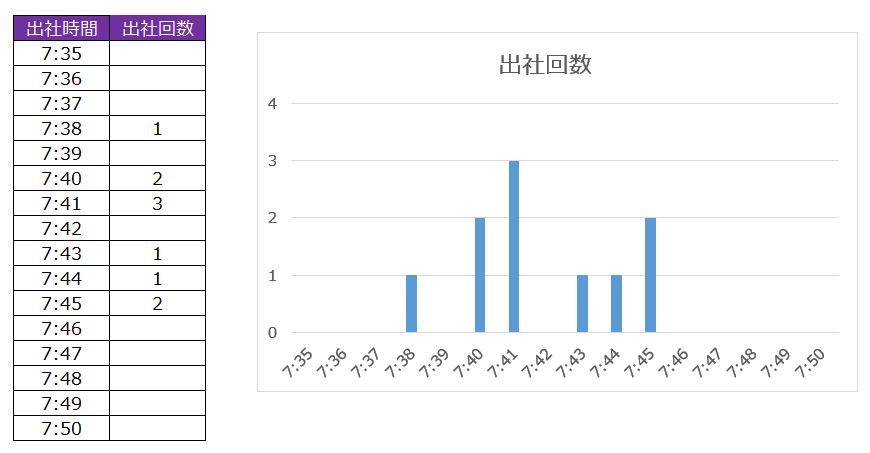
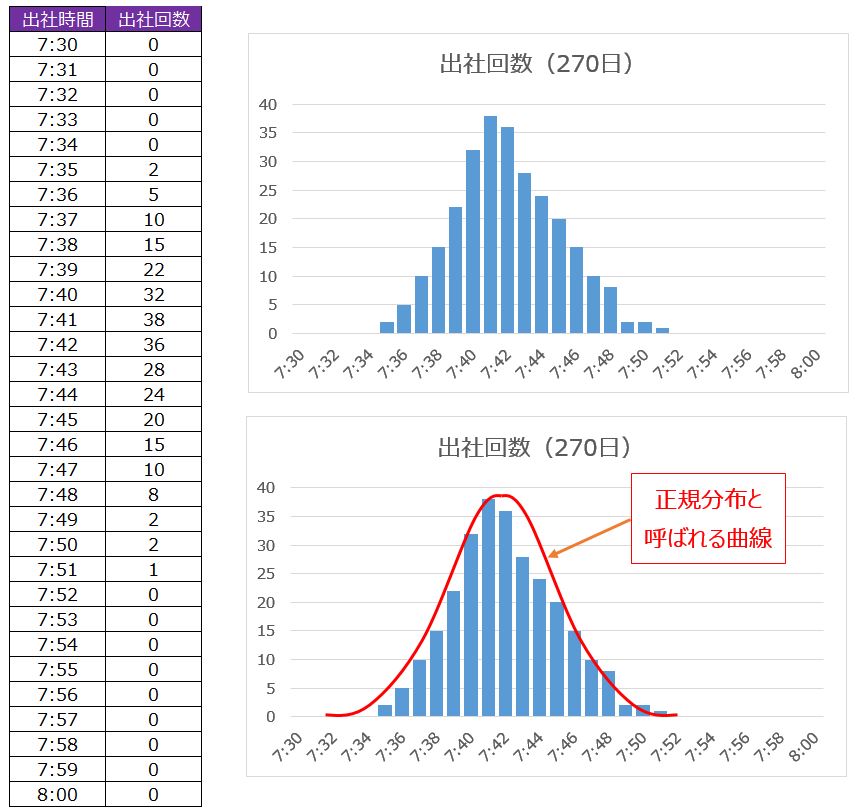
下の表とグラフは「何時何分に何回出社した?」です。
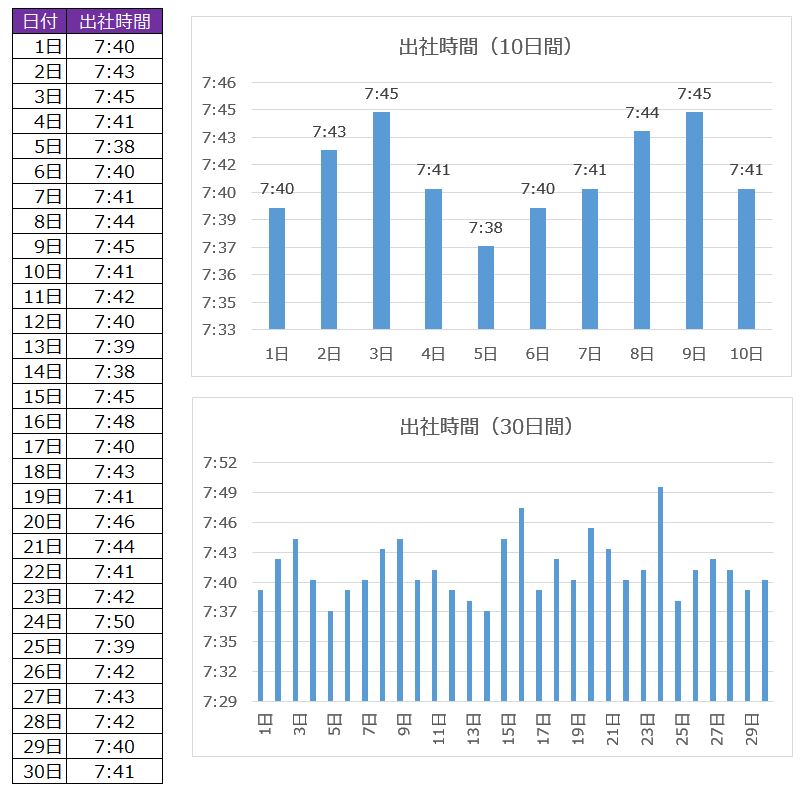
同じような見方で1ヶ月(30日)のデータにしてみます。
同じようなデータが並びます。(休みありませんが、気にしないで下さい^^;)
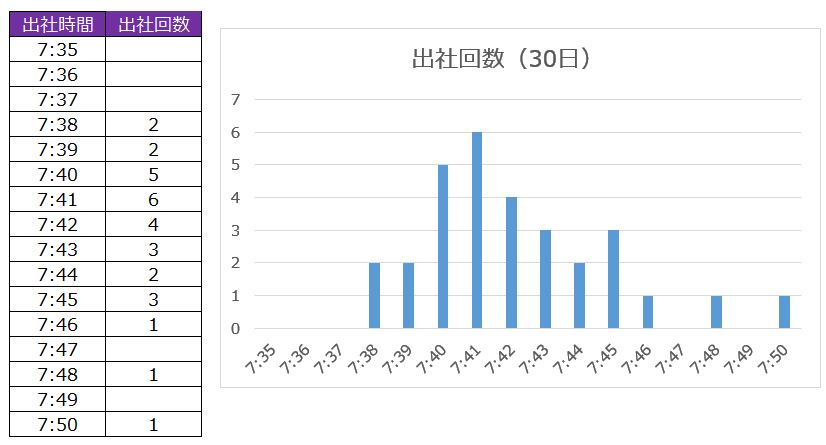
これを「何時何分に何回出社した?」に変換します。
少し山のように見えてきたと思います。
出社時間のデータをどんどん追加していくと「 山 」ができてきます。
下のグラフを見ると、7時に家を出てだいたい7時41~42分に到着してます。遅い日でも7時51分、早い日で7時35分ですが、あまり回数は多くありません。
この山のように見えるものを「正規分布」と呼びます。


バラツキって何?
正規分布のグラフで、曲線のように見える山の幅のことをバラツキと呼びます。
グラフを見ると、7時40~42分に会社に到着しますが、早い日で7時35分、遅い日は7時51分があります。
確率の話
出勤の早い日、遅い日はありますが、その回数は多くありません。
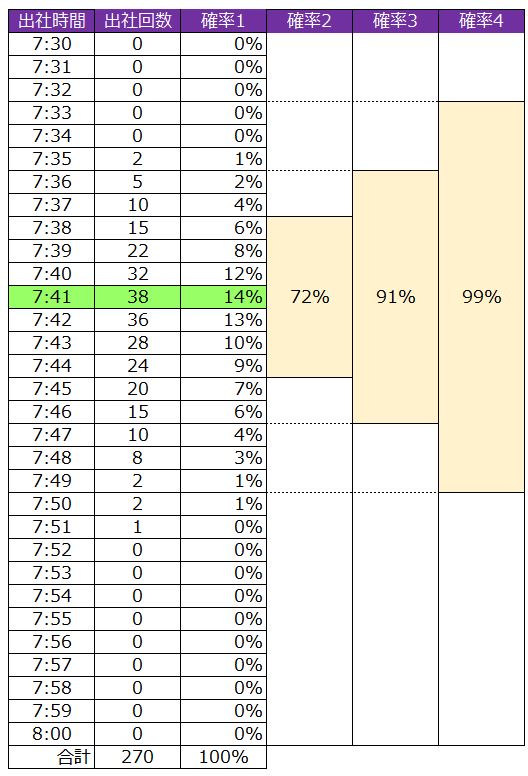
下の表の「確率1」の列にそれぞれの割合を計算してみました。「確率2~4」は、ある時間帯を合計したものです。
- 確率1の欄を見ると
-
7時41分の確率が1番高くて、全体の14%
- 確率2の欄を見ると
-
7時38分~7時44分までの合計が、72%です。
これは7時に家を出ると72%の確率で、7時38~44分に着くことを意味します。
- 確率3の欄を見ると
-
91%の確率で、7時36~46分に会社に着く
- 確率4の欄を見ると
-
99%の確率で、7時33~49分に会社に着くことが分かります
ここで、山のグラフを出社回数から、出社時間の確率に変えてみます。
でも、正規分布の曲線は変わらないことが分かります。
僕もそうですが、過去の経験(実績)から家を出る時間を決めてると思います。
このように、過去のデータに基づいて未来を予測する・物事を決めることを「統計学」と呼んだりします。
統計学に興味がある人は、下の本が読みやすいです。初心者向けの本は、Kindle unlimitedに加入してる人なら無料で読めます。
初心者の人に向けて書かれた本
中級者の人に向けて書かれた本
Kindle unlimited
- 初回30日間は無料体験
- 200万冊以上が読み放題
- 2ヶ月目から月額980円
- いつでも簡単に解約可能
\ 初回30日は無料 /
Kindle unlimitedの体験談は、こちらの記事で紹介してます。
σ(シグマ)って何?
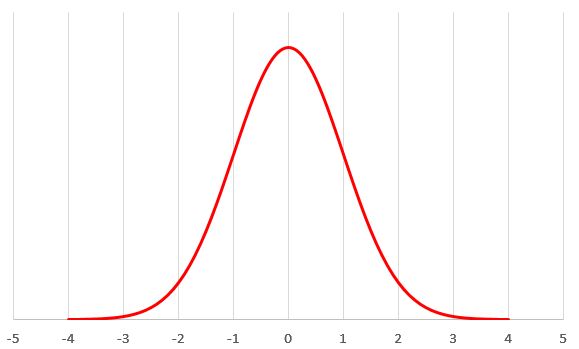
出社時間のグラフから正規分布の曲線だけを取り出して考えてみます。
計算から描くことができる、キレイな正規分布の曲線が下のグラフになります。
この曲線を計算する式があるのですが、ここでは割愛です(^^;;
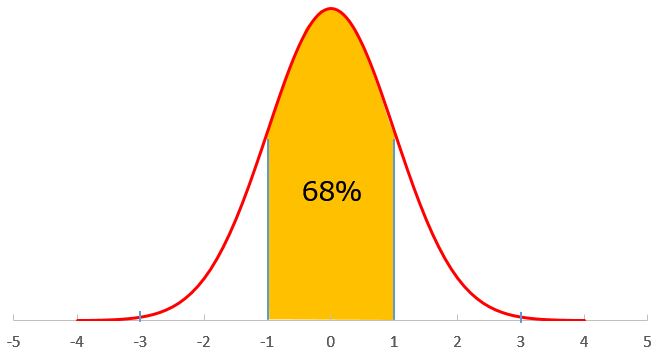
この曲線の「-1~0~+1」までの面積を計算すると全体の約68%になります。
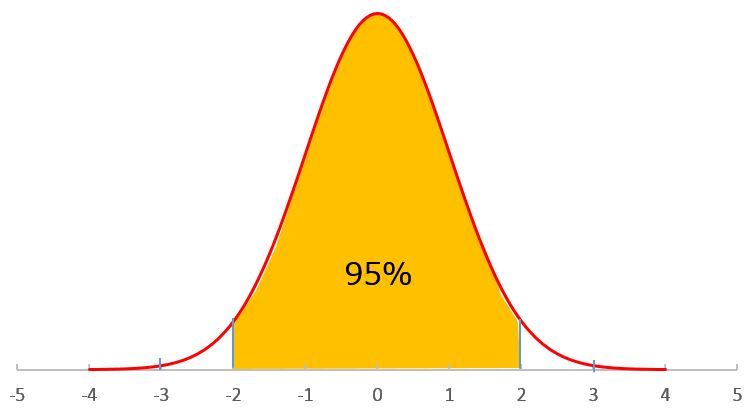
同じように「-2~0~+2」までの面積を計算すると全体の約95%になります。
- 同じように「-3~0~+3」の面積は、約99.7%
- 「-4~0~+4」の面積は、約99.994%と、どんどん100%に近づいていきます。
- このグラフの「1」を「1σ(シグマ)」と呼びます。
- 「-1~0~+1」の範囲を「±1σ」(1を省略して、±σ)
- 「-2~0~+2」の範囲を「±2σ」
- 「-3~0~+3」の範囲を「±3σ」と呼ばれています。
σ(シグマ)は、「標準偏差」とも呼ばれます。
σ(シグマ)は、「正規分布のバラツキを表現する単位」になります。
σ(シグマ)と正規分布の確率表
| σの範囲 | 範囲の中に入る確率 | 範囲から外れる確率 |
|---|---|---|
| ±σ | 68.3% | 31.7% |
| ±2σ | 95.4% | 4.55% |
| ±3σ | 99.73% | 0.269% |
| ±4σ | 99.993% | 0.0063% |
| ±5σ | 99.99994% | 0.000057% |
| ±6σ | 99.9999998% | 0.00000019% |
Excel(エクセル)での計算方法
σ(シグマ)はExcelを使って簡単に計算することができます。
出社時間30日を例にσ(シグマ)を計算してみます。
Excel関数の「STDEV.P」を使用します。少し古いExcelだと「STDEVP」です。
30日間の出社時間だとバラツキσは、2分46秒になります。2σはバラツキσの値を2倍、3σは3倍すればOKです。
このσ、2σ、3σの値を出社の平均時間7時42分8秒にプラス、マイナスして、結果をグラフに反映してみます。
この結果では、明日の出社時間は7時39~44分が、68%の確率になります。
まとめ
- 正規分布とは?
-
- ある値を中心に山のように見える曲線です。
- バラツキとは?
-
- ある値を中心として山のように見える曲線の幅です。
- σ(シグマ)とは?
-
- 正規分布のバラツキを表現する単位です。
工程管理を行う上での基本的な考え方となる正規分布について、少しでも理解頂けたらと思います。
正規分布の考え方を使った工程能力Cpの解説はこちら


最後までお付き合い、ありがとうございました。m(_ _)m